70以上 三角形 線分比 209784

線彼此之間也都互有關連, 它們相互架構出 一套完整的推理系統及美麗的幾何圖形。 比例三角形原本只是一個簡單的作圖方 法, 但只需要拿把直尺一比, 就會發現有平行 線及共線點在這單純的圖形中, 等這些性質 被推理證明後, 又由它們製造出新的平行線註1：內分比與外分比需作輔助線，內分比往 外作輔助線，外分比往 內作輔助線，再使用與平行有關的性質即可求證。 註2：三角形的內心可使用內分比性質求得。 內分比與三角形的內心 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは

外分比 Lekovi

三角形 線分比

三角形 線分比- 學校教過的數學法則當中，最簡單巧妙的大概就是「三角形的三個角加起來永遠是180度」。永遠是對的，沒有例外。但是（你可能會想坐著聽我接下來要講的事），學校騙了你。三角形的三個角加起來不會永遠是180度，而且證據一直在你眼前。 標籤 歐氏幾何, 數學, 三角形, 球面幾何三角形內的比例線段 (五) 劉俊傑 一 前言 大約十年前, 筆者曾在數學傳播第十九卷第二期中, 以 「三角形內的比例線段」 為題, 寫過 一篇短文 1。 該文的主要內容, 是從 Menelaus 定理出發, 建立了一套三角形

三角形的內分比性質 翰林雲端學院

影片：證明重心位於中線的2/3 (英)，khan videos > 三角形。源自於：均一教育平台 願 每個孩子都成為終身學習者，成就自己的未來。（證券）五分鐘 k 線足分計算： 設定證券的五分鐘 k 線第一根 k 棒，是否要計算到 905 策略： cci 訊號 順勢指標： 以 cci大於買進值 (預設 100)為買進訊號；小於賣出值 (預設 100)為賣出訊號。 dmi 訊號本页面最后修订于21年8月19日 (星期四) 0339。 本站的全部文字在知识共享 署名相同方式共享 30协议 之条款下提供，附加条款亦可能应用。 （请参阅使用条款） Wikipedia®和维基百科标志是维基媒体基金会的注册商标；维基™是维基媒体基金会的商标。 维基媒体基金会是按美国国內稅收法501(c)(3

 熱門文章 30萬人在臉書上按讚的英文漫畫：人生的意義 1,951,264 view;ベクトルと三角関数で表した内心，外心，重心，垂心 予備知識1 線分 AB を mn に内分する点 P の位置ベクトル は ※ に掛ける数は，図での見かけ上遠い方の長さ n ， に掛ける数は，図での見かけ上遠い方の長さ m となっていることに注意（「いじ悪な 二等辺三角形とは？定義 二等辺三角形とは、 \(\bf{2}\) つの辺の長さが等しい三角形 のことです。 二等辺三角形の等しい \(2\) 辺の間の角のことを「頂角」、その他の \(2\) つの角のことを「底角」といいます。そして、頂角に向かい合う辺のことを「底辺」といいます。

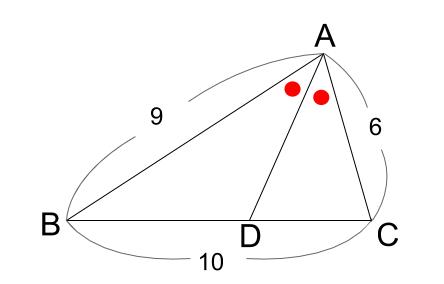
 先求 BC 三角形的西瓦綠長與斯特瓦特定理 A 具來解決這個問題，或是接下來要介紹的 就是國中學生可以瞭解的斯特瓦特定理。 這個定理是蘇格蘭數學家 6, 恥1atthew m Stewart 在西元 1975 年發表，用來求解三 角形中西瓦線段的長度 O B MEH C 7 斯特瓦特定理 L 辺の比の関係式は内角の二等分線とまったく同じなので、別々に暗記する必要はありません。 ただし、二等分線と向かい合う辺の交点の位置が 元の \(\triangle \mathrm{ABC}\) の外側にある ことに注意しておきましょう。 角の二等分線の性質三角形內的比例線段 劉俊傑 一 前言 比例的性質在幾何學中, 扮演著相當重 要的角色, 舉凡相似形、 平行線的截線、 角平 分線定理、 圓冪定理、 阿波羅尼斯圓、 托勒密 定理、 黃金分割等, 都能見到比例的蹤影 1。 而在近世幾何學, 比例更被廣泛地用來討論

北师大版九上数学4 2 平行线分线段成比例知识点精讲 腾讯新闻

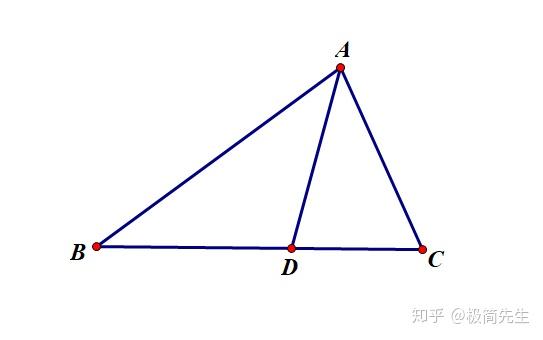
题型 解三角形 角分线 知乎

5 三角形 51 三角形 161 認識各種三角形 52 正三角形和等腰三角形 161 認識各種三角形 53 直角、銳角和鈍角三角形 144 認識直角 161 認識各種三角形 54 全等圖形與全等三角形 164 全等圖形 6 整數四則計算 61 加與減的併式 2294 有括號的加減併式 2平行線と線分の比 まとめ 以上、7パターンの問題について解説してきました。 おそらくこれらのパターンをしっかりと理解できていれば ほとんどの問題には対応できるのではないかと思います。 比の取り方は、練習で身につけていくのが一番です。平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\)

１ の証明を教えて下さい Clearnote

三角形頂點和邊三等分點連線所圍區域面積

 「2つの三角形が底辺が共通ならば面積比が高さの比と一致する」 という原理を使って対角線分割を説明することもできます。 上の図では abdと cbdは，共にbdを底辺とみなすこともできます。 そうすると面積比は高さの比になりますよね。 3分で分かる！直角二等辺三角形の定義・性質・証明などについてわかりやすく 数学 2 3分で分かる！最小公倍数とは？4通りの求め方も紹介！ 数学 724 3分で分かる！因数分解の公式と解き方のコツ・練習問題と解説をわかりやすく五、課本 在三角形中，以細繩懸吊三角形頂點，當三角形平衡時，懸線除了通過 其重心之外，也必平分三角形面積。 聯想5 若懸吊非三角形頂點，當三角形平衡時，根據物理學，懸吊線雖必通過 其重心，那懸吊線會平分三角形的面積嗎？

相似三角形的應用 題型解析 顧震宇台灣數位學習科技股份有限公司這個單元老師講解變數與函數的題型解析 Ppt Download

名師課輔網 內分比性質

Q＆A ─ 說明直角三角形的外心與重心共線 0014 37 祝學習成功 附件 長度 01, 發表時間 25 觀看次數 6,197 附件 討論功能僅開放給課程成員，請先加入課程 單元 13 正弦定理、餘弦定理, 「在夜深人靜之時，Po一下筆記好了🤣🤣 有人嗎？(・ω・)ノ 本筆記為三角函數章節之內容 形來中線比、角分源線比都等於相似比 比如：三角形abc和三角形def相似 abde=bcef=cafd ag、dh分別是兩個三角形的中線， 則bg=bc/2 eh=ef/2 bgeh=bcef=abde 角abg=角deh所以三角形abg與三角形deh相似 所以 agdh=abde 如果ag和dh是角分線，也可證明

2つの線分の交点の位置ベクトルや内分比を求める裏技 教師用

跟三角形中線 角平分線 高線有關的常見模型和結論總結 每日頭條

三角形の角の二等分線と辺の比の証明 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 このテキストでは、この定理を証明します。 次に、下図のように頂点Cを通り 直線ADと平行な直線 をひく。 の二等辺三角形(二)三角形之三內角平分線共點(內心)問題，並求證內心坐標。 (三)三角形一內角平分線及另兩角的外角角平分線共點(旁心)問題，並求證旁心坐標。 (四)三角形三高線共點(垂心)問題，並求證垂心坐標。 (五)三角形三邊中垂線共點(外心)問題，並求證外心坐標。 直角三角形abcにおいては、 bd：dc＝ab²：ac² でした。 したがって、 bd：dc＝169：81 です。 2乗すればいいだけですね。簡単です。 三平方の定理など他にもいくつかの方法で解くことができますが、これを知っていれば数秒で終わります。

三角形的內分比性質 翰林雲端學院

中考热点 平行线分线段成比例

 最後に、平行線と線分の比から $$\begin{eqnarray}ABAE(AC)=BDDC \end{eqnarray}$$ となります。 まとめ！ お疲れ様でした！ 内角の二等分線と比の性質は入試でもよく出題されます。 なので、絶対に覚えておきたいですね。三角形的基本性質 218 1 如右圖中，直線 ph 是 pqr 的對稱軸， pq ≠ rq ， m 是 pq 中點。 下列哪一個選項是錯誤 的？ 90 年第一次 (a) mh = hq (b) mh // pr (c) mh = mp (d) pqh @ prh 重點 ：由對稱軸觀念引進三角形的全等FdData 中間期末：中学数学3 年：平行線 三角形と線分の比／平行線にはさまれた線分の比／平行線と線分比応用／ 三角形の角の二等分線と線分の比 ／中点連結定理：証明問題／長さ・角度の計算／全般／ FdData 中間期末製品版のご案内

xx春人教版数学九下272 相似三角形 同步检测3 Doc

基本圖形分析法專題 平行線型相似三角形 一 每日頭條

 垂直二等分線 三角形の外心の話をする前に、垂直二等分線についておさらいをしておきましょう。 線分 AB があったとき、 AB の中点を通り、 AB と垂直に交わる線のことを、線分 AB の垂直二等分線(perpendicular bisector) といいます。 上の図で、線分 AB の中点を M としたとき、直線 PM が垂直二等分平行線と線分の比 平行線と線分の比 1 pq//bc ⇔ apab = aqac 2 pq//bc ⇔ appb = aqqc 3 pq//bc ⇒ apab = pqbc a p q p q a b c b c ※3だけ逆は成り立たない。 角の二等分線と比 角の二等分線と比 1 abcの∠aの二等分線と辺bcとの 交点pは辺bcをabbcに内分する。三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。

角平分線比例中四級 Sfhy

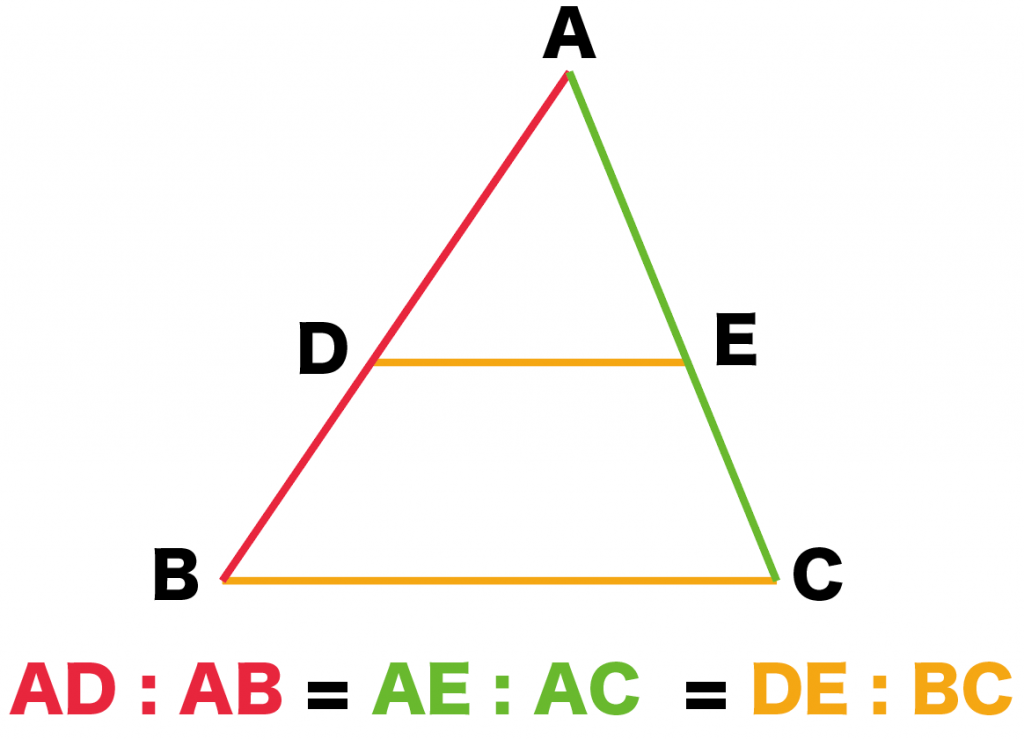
3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく

三角形的西瓦線長與斯特瓦特定理 21 7 ma h a 6 5 MEH A B C 本題先求高AH ，為此可令BH x ， CH x 7 ，利用畢氏定理可得 2 x x 2 求得 30 7 BH x ，再用 畢氏定理求得高 2 662 30 12 77 AH 若要再求中線AM ，這時可利用直角 AMH 畢氏定理。 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。簡單版 全文 72 截三角形兩邊的對應線段成比例之直線與三角形的第三條邊平行 簡單版 全文 71 與三角形一邊平行的直線截其它兩邊所得的對應線段成比例 簡單版 全文 70 等高的三角形面積的比等於底的

基本圖形分析法專題 平行線型相似三角形 二 雪花新闻

平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題

三、畫畫看(每題3分，共6分) 1以 4 1 為刻度單位，畫出2 到3 之間， 標示有分數的數線。 2以虛線為對稱軸，畫出下面線對稱圖形 的另一半： 四、把做法和答案記下來(每題4分，共24分) 溫馨的耶誕節即將來臨，成德百貨公司陸 續展開一系列的耶誕活動。

1

請問不用內分比的話要如何解這二題 謝謝 Clearnote

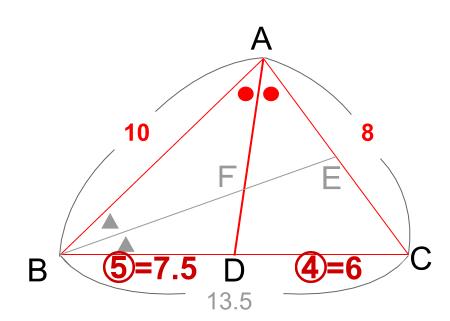
角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su

利用平行線構造相似三角形 用這道題來訓練效果最好 每日頭條

直角三角形における線分の比 思考力を鍛える数学

角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典

三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア

数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ

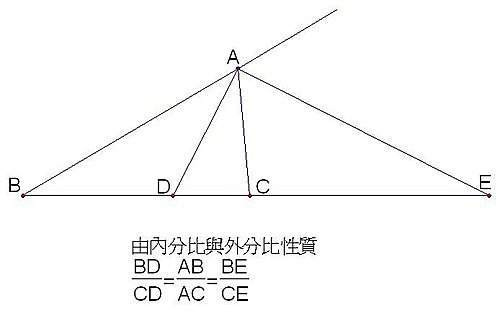
調和點列 老王的夢田 痞客邦

跟三角形中線 角平分線 高線有關的常見模型和結論總結 每日頭條

重心线段比例证明 重心分中线成两段 它们的长度比为2 1 怎么证明 三人行教育网 Www 3rxing Org

相似三角形知识点与经典题型 沃文网wodocx Com

內分比與外分比 Go East Go West Or Go To Rest 隨意窩xuite日誌

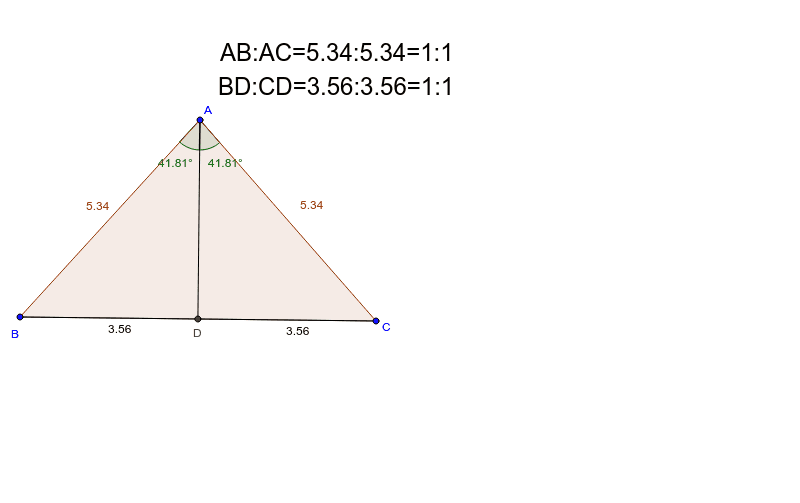
角の二等分線と線分の比 Geogebra

1

如果您有一个等腰三角形 其底脚等于无穷大 那是否意味着斜边会大于无穷大 教育小本子

三等分点连线围成的小三角形 哔哩哔哩 Bilibili

分得三角形面積比為1 2 3的點探究和拓展 每日頭條

求解拜託不要略過 Clearnote

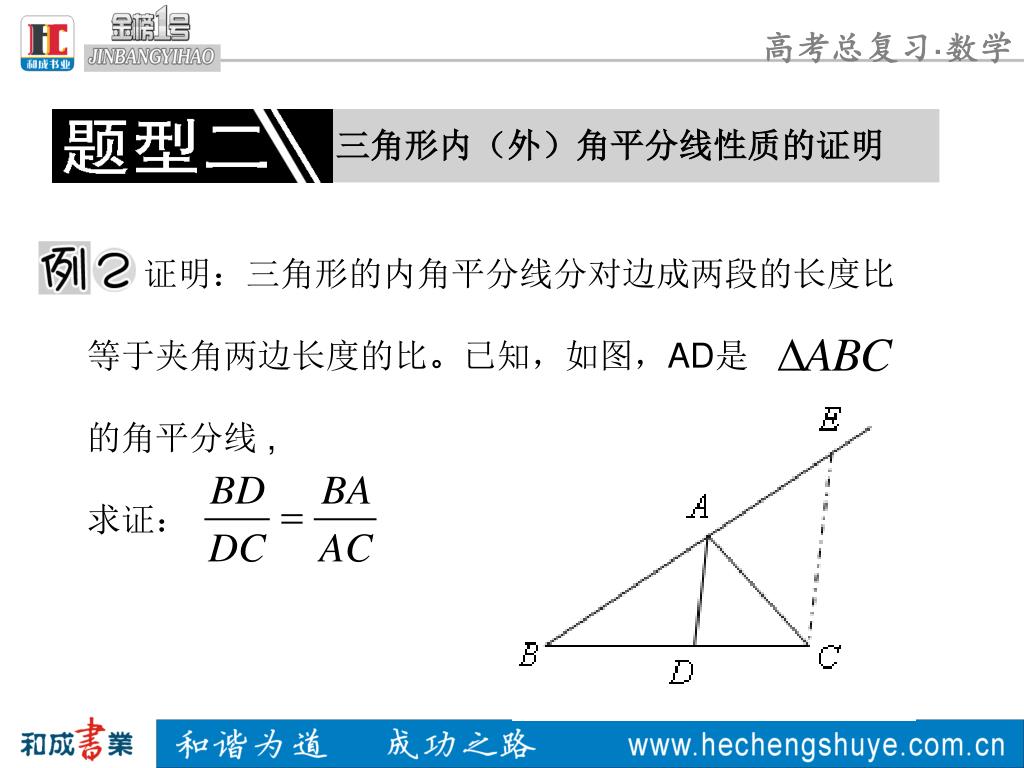
Ppt 第一讲几何证明选讲powerpoint Presentation Free Download Id

三角形內分比 外分比定理 Easy Math Club

內 外分點公式證明 信欣茗數學園地 隨意窩xuite日誌

Abc三边长分别是3 4 6 则它的较大锐角的平分线分三角形的面积比是 雨露学习互助

證明例題 角平分線分割對邊比 內分比 Live 多媒體數學觀念典online

外角平分線 Feno

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

輔助線技巧利用二倍角構造等腰三角形 技巧比努力更加重要 每日頭條

波提思互動數學教學 內分比的觀念 Youtube

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中３ ２０ １ 線分比と面積比 １ Youtube

三角形內分比 外分比定理 Easy Math Club

三角形的內分比性質diagram Quizlet

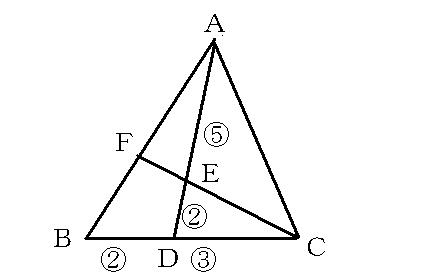
線分の長さの比 １ 受験勉強のコーヒーブレーク

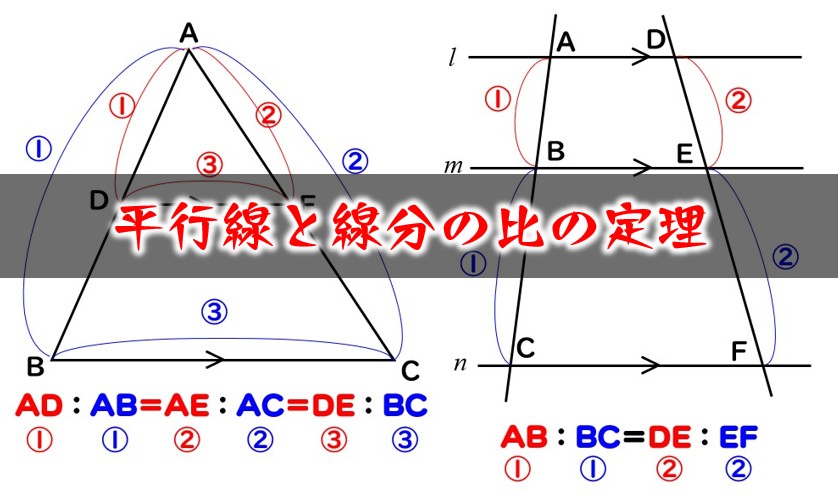
平行線と線分の比の定理 の問題の解き方 数学fun

思维导图解题课件范例 年湖南省常德市中考数学几何压轴题 小初高题库试卷课件教案网

內分比性質 Youtube

初中數學相似三角形知識點總結及解題技巧 沒有掌握的同學進來看 每日頭條

中学３年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

日本eju留考数学精讲丨三角形内角平分线定理的证明方法 哔哩哔哩 Bilibili

中学3年数学 相似の応用 線分比の移動 Youtube

平行线分线段成比例定理与三角形一边的平行线 含分式的合比 分比 合分比性质 哔哩哔哩

孟氏定理西瓦定理平面幾何新路 Mrsysy

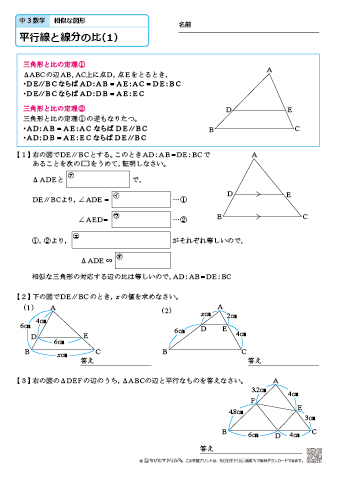
中学３年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生

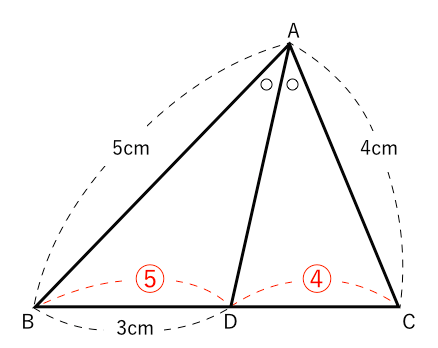
相似な図形 角の二等分があったらこれ 苦手な数学を簡単に

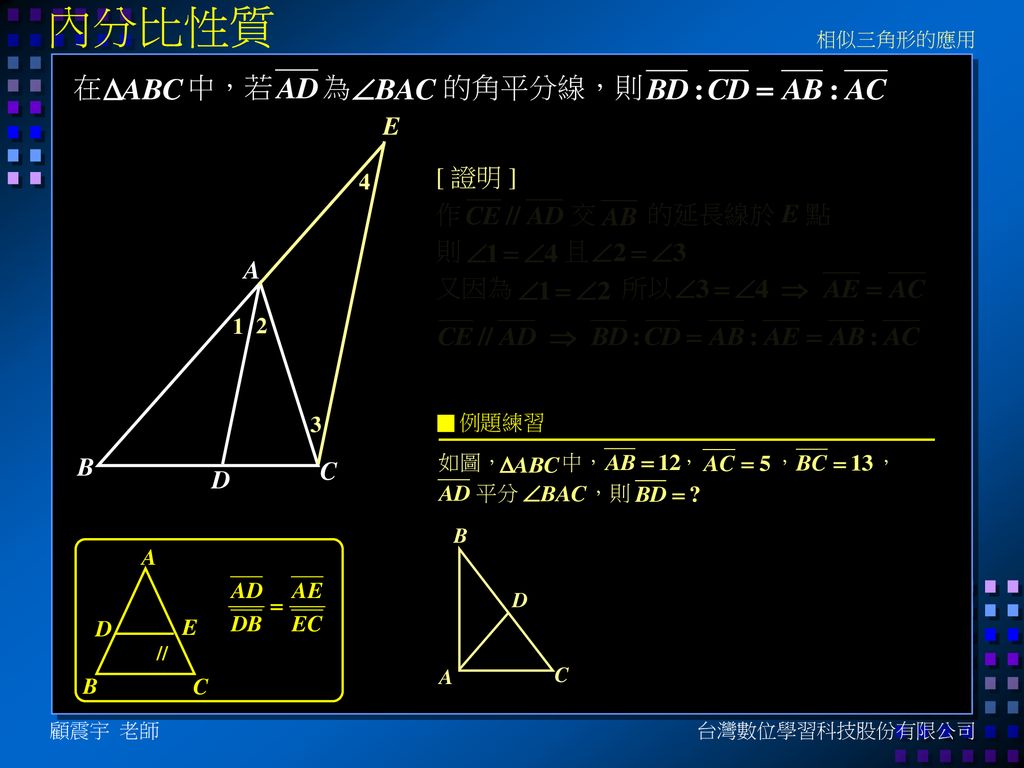
大綱 母子相似性質內 外分比性質重點複習顧震宇台灣數位學習科技股份有限公司 Ppt Download

內分比性質 Youtube

內分比與外分比 Go East Go West Or Go To Rest 隨意窩xuite日誌

数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生

分得三角形面積比為1 2 3的點探究和拓展 M頭條

角平分線性質角平分線性質 Pweon

Fines 高校受験対策講座 数学 線分比と面積比 Youtube

三角形の面積比なんですが なぜ線分の割合で面積が決まるんでしょうか Yahoo 知恵袋

內分比性質 Youtube

几何基础 三角形之重心分中线为2比1 腾讯视频

外分比 Lekovi

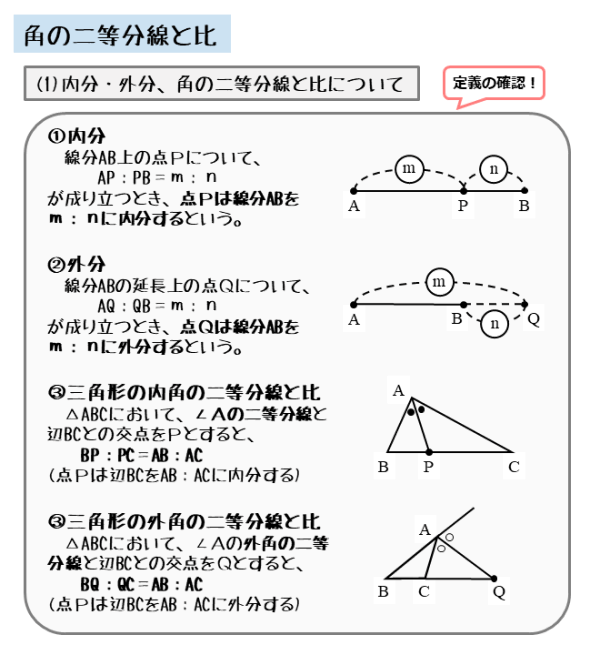
図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん

相似知识点总结 相似知识点总结精选八篇 范文118

Studydoctor平行線と線分の比の利用 中３数学 Studydoctor

角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su

中3数学 相似と線分比１ 平行四辺形 Youtube

分角線分角線 Byaml

五六年級數學 新信息給予題 理解了秒解 面積比 線段長比 每日頭條

角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su

三角形比例線段

北师大版九上数学4 2 平行线分线段成比例知识点精讲 腾讯新闻

18年中考數學百日衝刺快速提分秘笈之相似與位似的解題妙招 壹讀

サクッと解説 角の二等分線と比の特徴となぜ について 数スタ

4 明郁在寫三角形內分比性質證明的時候 不小心有幾行被弟弟擦掉了 已知被擦掉的那 阿摩線上測驗

證明例題 角平分線分割對邊比 內分比 Live 多媒體數學觀念典online

三角形的內心座標instagram Posts Gramho Com

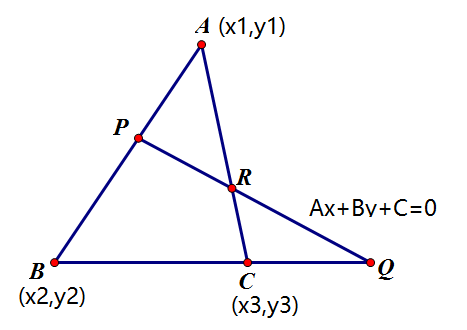
定比分点公式及定理 定点分比公式的推导 男霸网

初中数学 相似三角形13大知识点 6大经典例题解析 先保存 楠木轩

內分比與外分比 Go East Go West Or Go To Rest 隨意窩xuite日誌

数学 中3 49 平行線と線分の比 基本編 Youtube

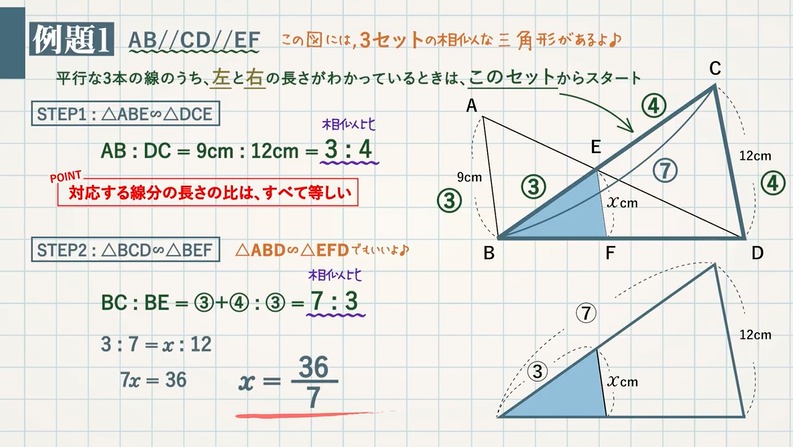
平行線と線分の比 辺の長さを求める応用問題４選 教遊者

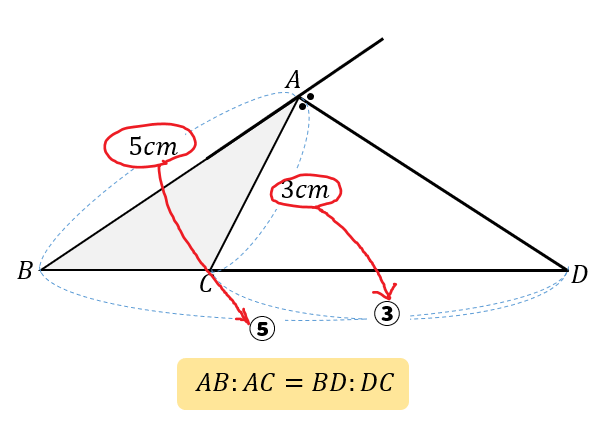
サクッと解説 角の二等分線と比の特徴となぜ について 数スタ

北师大版九上数学4 2 平行线分线段成比例知识点精讲 腾讯新闻

內分比與外分比 Go East Go West Or Go To Rest 隨意窩xuite日誌

陳彥銘數學 外分比性質的證明 Facebook

射影幾何 分角線引理 老王的夢田 痞客邦

思维导图解题课件范例 年湖南省常德市中考数学几何压轴题 小初高题库试卷课件教案网

例題 三角形的內分比 2 數學 均一教育平台

1

角平分線比例中四級 Sfhy

瓊花寶典 痞客邦

初一数学 9 3 三角形的角平分线 中线和高 中考知识点解读

数学 三角形の辺と面積の比について ２つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生